|
Feb.
27 2007
Detecting
and analyzing higher dimensions
via
the EM radiation field
by Hans de Vries
|
|
Modern day theoretical physics and higher dimensions.
|
|
The
very successful "Standard Model" in
theoretical physics was established in the seventies and the
eighties. It united the Electromagnetic force with the Weak and
the Strong nuclear force. This model could predict the outcome
of numerous
experiments
performed at the large particle accelerators which were probing
the mysteries of Nature.
A
major part of the physics community, then full of confidence,
went on to study models embracing both the Standard Model and
Einstein General theory of relativity. These models, mostly referred
to as "String Theory" have a remarkable aspect:
They
presume
extra spatial dimension above our three current ones.
The
successful years of the Standard Model in which rapid
developments came one after the other has turned in a silent
period now for more then two decades without real results. Was
the assumption of higher dimensional spaces to speculative? Can
we ever hope to probe these higher dimension? Can we disprove
their existence?
| The
higher dimensional String Theory is undergoing somewhat of
a crisis, even while scoring huge successes on the public
relation front. A startling example:
The Chinese government,
always keen on new knowledge and technology, opened up the
symbolic center of its power: Beijing's Great Hall
of the People, the meeting place of the communist party,
to host the yearly conference on string theory in the
summer of 2006.
It also
invited around 3000 of its brightest and most intelligent
students to attend the meeting in an apparent attempt to
create an 'army' of new string theorist.
|
|

Higher
Dimensional Theories in
Beijing's
Great Hall of the People |
|
|
Higher dimensional Electro Magnetic fields.
|
|
In
this paper we derive and describe how the EM field looks like in
an arbitrary higher dimensional space. It strongly suggest that
we should have seen signs from these higher dimensions already,
that is, if they exist. We should have seen the effects directly
via the nature of the electromagnetic radiation originating from
charges moving and accelerating within these higher dimensions.
How
can we derive the behavior of the EM fields in
higher dimensions? It turns out that we can go from,
say, a four or five dimensional space to 3d, in the same
way as we go from 3D to a one or two dimensional
space.
A
two dimensional (x,y) space looks in 3D as a collection of
parallel lines, infinitely extended into the z direction,
while a one dimensional (x) space looks like a collection
of planes infinitely extended into the y and z directions.
This
means that the n-dimensional EM field, must always produce
the laws of physics, as we know them, in 3D space when we
extend the objects in n-dimensional dimensions in the same
way as we have to do when we go from 3D to 2D or
1D.
One
very remarkable difference one finds, is how the magnetic
field of a particle depends on the speed and acceleration
of the charge. In 3D space the magnetic field is
proportional to the speed of the charge (the current). In
higher dimensional spaces one finds a very different
relation.
The
largest term is dependent on a higher derivative of the
speed. See the image on the right. The particle's speed is
given in all situations by a smooth curve, made out of
parabolic curves. Starting with v=0, then gradually accelerating
and de-accelerating again to a standstill.
In
3D the charge will generate a magnetic field which is
proportional to the speed. In 5D however the largest term
of the magnetic field is proportional to the acceleration
of the charge. This is basically a triangular pulse since
the motion of the charge is following a curve made out of
parabolic curves.
|
|
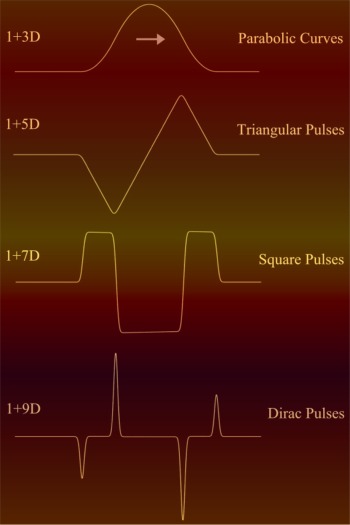
Magnetic
field of a particle moving with the same speed the same
way but in different higher dimensional spaces. |
In
9D space, which together with the time dimension, is the usual
10 dimensional space associated with string theory we see even
stronger effects. The major component of the magnetic field B is
proportional to the third derivative of the speed. The
discontinuities were the separate parabolic curves are connected
together, hardly visible in the 3D situation, now become strong
Dirac pulses.
The
magnetic field and the radiation associated with it are very
different from that in the usual 3D space. This would
suggest that higher dimensions, even if they are compacted at
Planck's scale should produce measurable effects. Something which
hasn't been seen so far. Some newer versions avoid problems
by a priory stating that the Electromagnetic, the Weak and the
Strong nuclear force can only propagate in a limited 3D space,
(The 3D Brane theories) while gravitations would be able to
propagate in all 9 spatial dimensions. There still remain
problems with the latter since gravitons which are considered
being mass less, have similar propagators as the ones described
in the paper ( ref[3] ) and similar effects occur for the
gravito magnetic fields.
|
|
The paper.
|
|
|
The
paper itself can be accessed by clicking on the PDF logo. It
requires a graduate physics level for a good understanding. Care
has been taken to make it accessible as possible. As often
happens, after finishing the document I found out that much of
the paper isn't really original work. It is mentioned that a
full derivation mass less propagators in the space-time domain
of any dimension is also given in reference [1]. Reverences [2]
and [3] show identical results as we do. Interestingly,
reference [3] discusses gravitons instead of photons. The correspondence
is of course the result of both having mass less propagators
with the difference that the gravitons correspond to a spin 2
tensor field and the photons to a spin 1 vector field.
|
|
 |
|
|
Other sources
|
|
[1]
S. Hassani, Mathematical Physics, (Springer-Verlag, New York,
1998)
Is
mentioned to contain a complete derivation of the massless
propagators in the space-time domain in any dimensional space.
[2]
D. V. Gal'tsov, Radiation reaction in various dimensions,
Physical Review D 66, 025016 (2002). hep-th/0112110
http://arxiv.org/PS_cache/hep-th/pdf/0112/0112110.pdf
[3] Cardoso et. al. Gravitational Radiation in D-dimensional
Spacetimes, Physical Review D 67 064026 (2003). hep-th/0212168
http://arxiv.org/PS_cache/hep-th/pdf/0212/0212168.pdf
|
|
|
|
Regards,
Hans
|
|
|
|
