October 4, 2004

An exact formula for the

Electro Magnetic coupling constant.

( fine structure constant )

  by Hans de Vries 

One of the most important numbers in physics is the electro magnetic coupling constant which defines the strength of the

electro-magnetic field. It is a dimensionless number independent of how we define our units of mass, length, time or electric charge. A change in these units of measurement leaves the dimensionless constant unchanged. 

The number can be seen as the chance that an electron emits or absorbs a photon. It enters modern physics as a non- linear term in the equations of Quantum Electro Dynamics. It is this non-linear term that allows wave packets to interact by exchanging photons.

 α   =   0.007297352568 (24)   =  1 / 137.03599911 

The value shown above is exact for the energy range in our daily life up to energies much higher than in the center of a nuclear explosion. The exactness of the constant is linked to that of the charge: Any effects at extremely high energies that change the effective value of the electric charge also change the value of the coupling constant. 

     An exact Formula. 

A fundamental question has long been if the number above can be expressed by a simple numerical formula like a combination of elementary values like π, e and small numbers, or that it has a more arbitrary value based on some underlying physical conditions.  

Even somebody like Feynman who was very well aware that the value could change at higher energies kept on proposing the search for such an expression (The Nobel Price won by Feynman was for work in which vacuum polarization and charge renormalization, issues responsible for the change of  the constant at extremely high energies, played an elementary role )

However, the search for such an elementary formula has more or less been given up nowadays. Proposed formulas generally needed six to eight arbitrary numbers to get an eight to nine digit result and don't look like anything seen in physics. The general consensus is now that the constant is just some arbitrary number based on underlying conditions.

Nevertheless, such a formula, if found, may have far reaching consequences. It would mean that the strength of the electro magnetic force in its relation to other forces is in the limit determined by geometry alone. This by itself would be one of the strongest possible hints that the forces of nature are all coming from a common physical source.

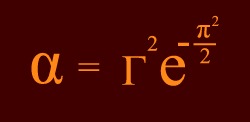
The formula above generates the value of α exact in all ten known digits. The term gamma is a small correction on the Gaussian exponential.  It can be expressed as a so-called radiative series in alpha. The series shows an elegant simplicity:

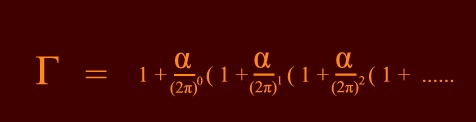
Expansion as a function of the powers of the coupling constant is a fundamental property of all Field Theories where

a term in αⁿ m is generally described by an nth order Feynman Diagram.  Terms like 1 + α / (2π) remind us of the famous QED calculation of the magnetic anomaly of the electron. This is the calculation meant when people say that Quantum Mechanics is tested with the highest precision of any physical theory. The calculation for the magnetic moment starts of with the term 1 + α / (2π) as found by Julius Schwinger in 1948.

The series converges to beyond experimental precession after the term n=3. We first fill in the measured value for α (which is 0.007297352568) in the series and look what value we obtain for pi in the right hand term. We see that it corresponds to the actual value of pi with a precision better than one in one hundred billion after term three !

Next we cut the series after N terms and use a simple iteration program to see which value it generates for α. We see that it becomes equal to the measured value until the very last digit after term 3 and further.  ( notwithstanding the given sigma ) 

 Regards,  Hans